5G LDPC - Lifting factor Zc
Overview
Lifting factor hay expansion factor \(Z_c\) (có nhiều tài liệu ký hiệu là \(Z\)) là tham số được sử dụng để quyết định kích thước của ma trận cơ sở (\(B\)) sẽ được mở rộng bao nhiêu lần. Việc sử dụng ma trận cơ sở \(B\) để mô tả parity check matrices là một phương pháp hiệu quả giúp giảm tài nguyên nhớ. Về mặt lý thuyết, phương pháp này giảm được \(Z^2_c\) phần tử nhớ (trong thực tế, tài nguyên nhớ sử dụng còn tiếp tục được tối ưu hơn nữa, do việc tính toán chỉ cần sử dụng một phần của ma trận cơ bản bao gồm ma trận \(A, E, C_1, C_2\)).
Phần sau sẽ mô tả cách tính \(Z_c\) được mô tả trong tài liệu 3GPP.
Compute \(Z_c\)
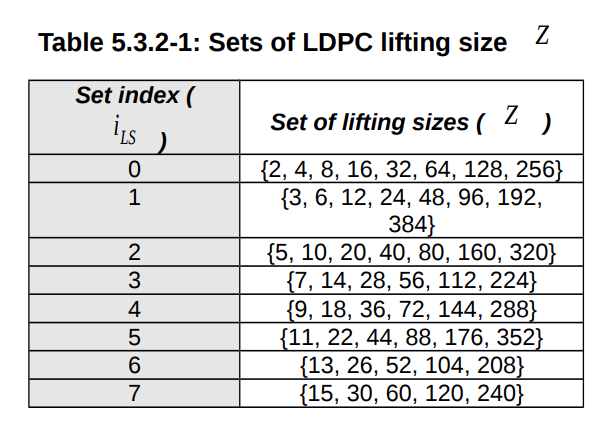
Mỗi \(i_{LS}\) index sẽ có nhiều giá trị có thể có của \(Z_c\).
Việc tính toán các giá trị của \(Z_c\) cho mỗi \(i_{LS}\) index được thự hiện như sau:
| Tham số | —– | —– | —– | —– | —– | —– | —– | —– |
|---|---|---|---|---|---|---|---|---|
| \(i_{LS}\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| \(a\) | 2 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| \(J_a\) | 7 | 7 | 6 | 5 | 5 | 5 | 4 | 4 |
Bảng trên được hiểu như sau:
-
Với index 0, trong đó \(a = 2\) thì \(J_a = 0, 1, 2, ..., 7\)
-
Với index 2, trong đó \(a = 5\) thì \(J_a = 0, 1, 2, ..., 6\) …
Với mỗi giá trị \(a\) hay với mỗi index \(i_{LS}\), thì:
\[Z_c = a * 2^{j_a}\]Như vậy table 5.3.2-1 đang mô tả các giá trị của \(Z_c\) ứng với mỗi index, nhưng bản chất nó là tập các giá trị của \(Z_c\) ứng với một giá trị của \(a\). Sau cùng, chúng ta sẽ chỉ quan tâm đến các giá trị của \(Z_c\) mà thôi.
\(Z_c\) selection
Việc lựa chọn \(Z_c\) phụ thuộc vào độ dài của thông tin cần mã hóa (theo đơn vị bit). Nó được mô tả ở phần Matlab code dưới đây.
Với mỗi \(Z_c\), ma trận cơ sở B sẽ có những ràng buộc sau đây:
- Giá trị của elements trong ma trận có giá trị \([-1, 0, .. Z_c-1]\)
- Các ma trận expansion thay thế cho các elements trong ma trận cơ sở sẽ luôn có kích thước Zc x Zc
- -1: tương ứng ma trận 0 kích thước Zc x Zc
- 0 : tương ứng với ma trận Identity kích thước Zc x Zc
- Các giá trị a lớn hơn 0: tương ứng với ma trận Identity được shift phải a lần
Matlab code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
% Find the minimum value of Z in all sets of lifting sizes in 38.212
% Table 5.3.2-1, denoted as Zc, such that Kb*Zc>=KdE1_CB
% Step 1: Determine Kb
% Step 2: Determine minimum value of Zc
% Kb is number of columns carrying actual information bit (no filler bits) in base matrix
if NBG == 1
Kb = 22;
else
if B > 640
Kb = 10;
elseif B > 560
Kb = 9;
elseif B > 192
Kb = 8;
else
Kb = 6;
end
end
Zlist = [2:16 18:2:32 36:4:64 72:8:112 120 128 144 160:16:256 288 320 352 384];
% Kd is length of each codeblock (excluding filler bits)
for Zc = Zlist
if Kb*Zc >= Kd
break;
end
end