5G LDPC - Base Matrices
Describing 5G LDPC base matrix and how to construct it
1. Overview
Ma trận cơ sở B là một trong những thông tin cần phải được hiểu rõ trong khi tìm hiểu giải thuật mã hóa và giải mã LDPC. Ma trận này khi được triển khai trên FPGA sẽ được lưu dưới dạng ROM, hay nói cách khác chúng sẽ được tính toán trước (pre-computed) thay vì tính toán on-fly. Phần dưới đây sẽ mô tả các đặc tính của một ma trận cơ sở cũng như cách chúng được xây dựng.
2. Base matrix (B) and parity check matrix (H)
Ma trận cơ sở B là một ma trận có kích thước như sau:
- Base graph 1: 46 hàng x 68 cột
- Base graph 2: 42 hàng x 52 cột
Ma trận H được tạo thành từ việc thay thế các phần tử của ma trận cơ sở B, bằng các ma trận có kích thước Zc x Zc. Cụ thể, các phần tử của ma trận cơ sở sẽ có một trong các giá trị sau và tương ứng là ma trận kích thước ZcxZc
| Giá trị | Ý nghĩa |
|---|---|
| -1 | Ignore <=> Ma trận 0 |
| 0 | Ma trận I (Identity matrix) |
| \(Zc > a > 0\) | Ma trận I được shift phải \(a\) lần |
Hình dưới đây là một ví dụ. Với expansion factor = 5 hay Zc = 5 (Một số tài liệu họ gọi là lifting factor hay có thể ký hiệu là Z). Chi tiết về Zc có thể xem tại đây.
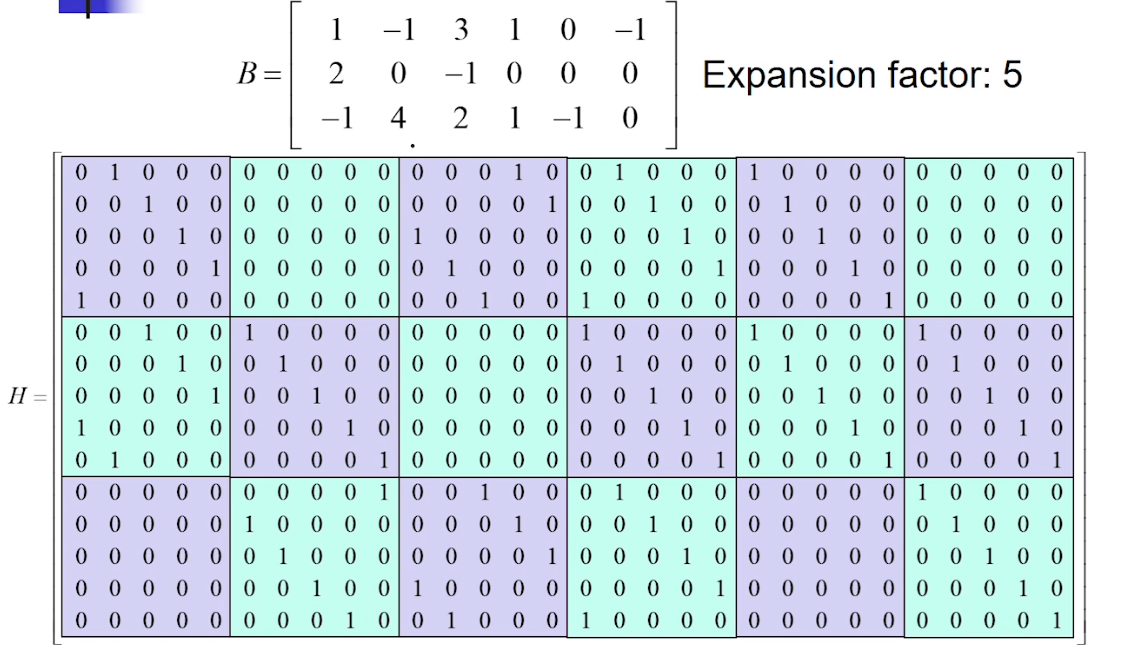
3. Base matrix structure
Ma trận cơ sở có kích thước khác nhau ứng với mỗi loại base graph. Tuy nhiên, chúng đều có chung một cấu trúc như sau:
\[B = \left[\begin{array}{cc} A & E & O \\ C_1 & C_2 & I \end{array}\right]\]Trong đó, kích thước của từng ma trận sẽ là:
| Ma trận | Base graph 1 | Base graph 2 |
|---|---|---|
| A | 4 x 22 | 4 x 10 |
| E | 4 x 4 | 4 x 4 |
| \(C_1\) | 42 x 22 | 38 x 10 |
| \(C_2\) | 42 x 4 | 38 x 4 |
| O | 4 x 42 | 4 x 38 |
| I | 42 x 42 | 38 x 38 |
Ma trận \(A, E\) được sử dụng để tính 4 parity bit đầu tiên (Ký hiệu: \(p_a\)).
Ma trận \(C_1, C_2\) được sử dụng cùng với 4 parity bit đầu tiên {\(p_{a_1}, p_{a_2}, p_{a_3}, p_{a_4}\)} để tính các parity bit còn lại (Ký hiệu: \(p_c\)).
Ma trận \(O, I\) có thể bỏ qua trong quá trình tính toán.
Để dễ hiểu hơn, ta có thể nhìn vào hình sau:
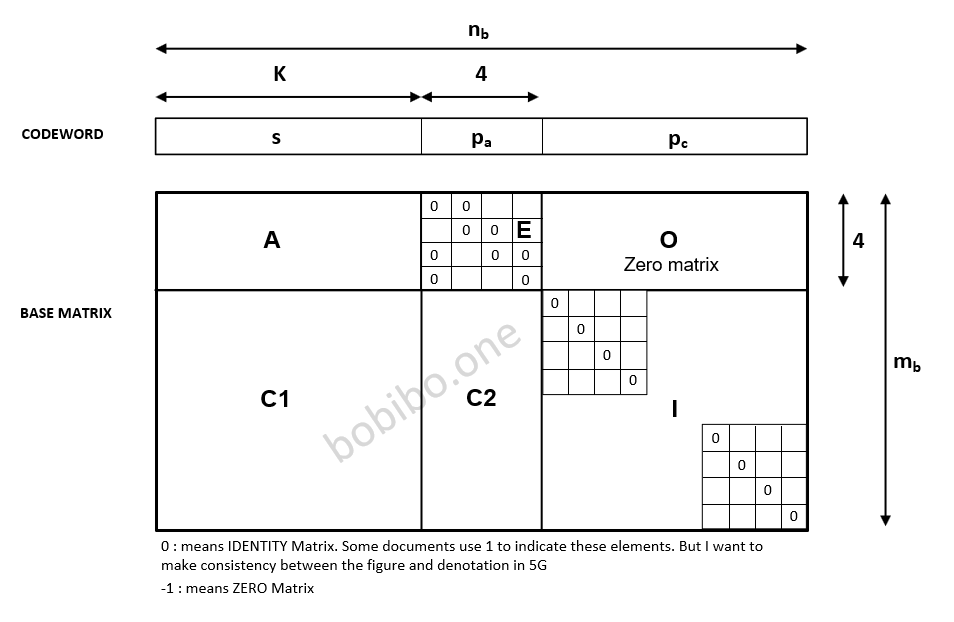
Ma trận \(E\) là một ma trận đặc biệt có tên gọi “Ma trận đường chéo đôi” (Double diagonal matrix). Đặc tính của ma trận này, giúp việc tính toán 4 parity bits (\(p_a\)) trở lên đơn giản và hiệu quả hơn. Cụ thể, quá trình tính toán sẽ được mô tả ở bài viết 5G LDPC encoder.
4. How to construct 5G LDPC base matrices
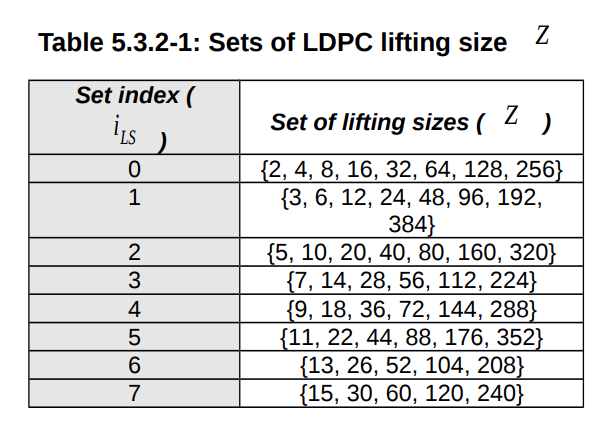
Ma trận cơ sở B sẽ được xây dựng dựa trên ba tham số { NBG, \(i_{LS}\), \(Z_{c}\) }
Từ tham số NBG và \(i_{LS}\), ta sử dụng bảng 5.3.2-2 và 5.3.2-3 trong 3GPP-38.212 (Section 5.3.2) để xây dựng lên base matrix cho giá trị \(Z_c\) lớn nhất.
Ví dụ
NBG = 2 (Base graph 2), \(i_{LS} = 6\). Tra theo bảng 5.3.2-3
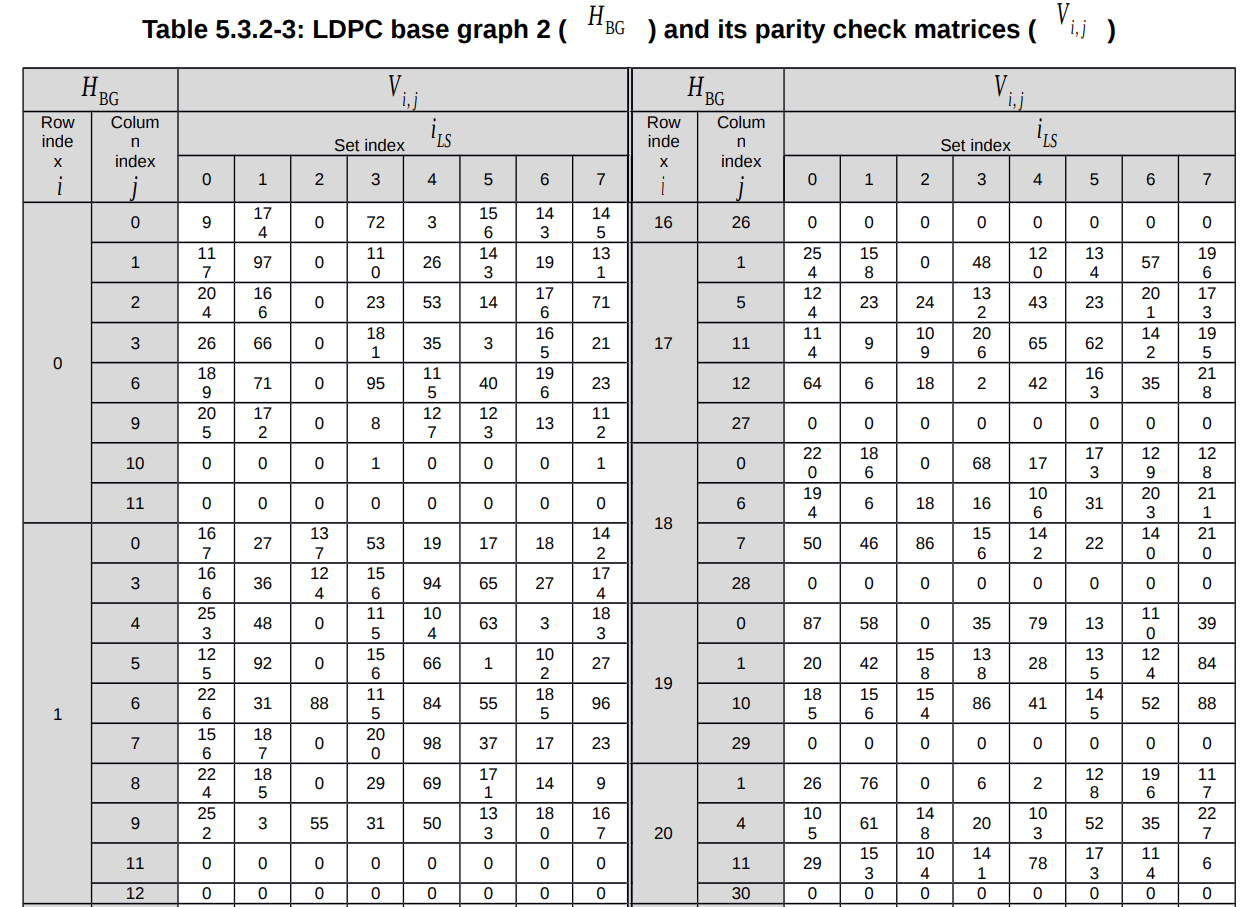
Ta sẽ có base matrix của \(Z_c = 208\) sẽ là:
\[B = \left[\begin{array}{cc} 143 & 19 & 176 & 165 & -1 & -1 & 196 & -1 & -1 & 13 & 0 & 0 & -1 & -1 & -1 & ... \\ 18 & -1 & -1 & 27 & 3 & 102 & 185 & 17 & 14 & 180 & -1 & 0 & 0 & -1 & -1 & ... \\ ... \end{array}\right]\]Với các trường hợp còn lại của \(Z_c = 13, 26, 52, 104\) ứng với \(i_{LS} = 6\). Giá trị của mỗi element sẽ được tính theo công thức:
\[b = a \bmod Zc (1)\]Trong đó:
- a là giá trị của element trong ma trận B ứng với \(Z_c\) lớn nhất
- b là giá trị của element của ma trận B ứng với \(Z_c\) cần tính
Khi \(Z_c = 13\) thì ma trận B sẽ trở thành:
\[B = \left[\begin{array}{cc} 0 & 6 & 7 & 9 & -1 & -1 & 1 & -1 & -1 & 0 & 0 & 0 & -1 & -1 & -1 & ... \\ 5 & -1 & -1 & 1 & 3 & 11 & 3 & 4 & 1 & 11 & -1 & 0 & 0 & -1 & -1 & ... \\ ... \end{array}\right]\]Kết luận
- Có 51 giá trị \(Z_c\), tương ứng sẽ có 51 ma trận cơ sở B với mỗi Base Graph. Do đó, 5G LDPC sẽ có tổng cộng 102 ma trận cơ sở. Việc thiết kế FPGA sẽ cần phải tối ưu việc lưu trữ các ma trận này để đảm bảo tiết kiệm tài nguyên nhớ và không bị “nghẽn cổ chai” khi thực thi việc mã hóa và giải mã.
- Trong thực tế, không cần phải lưu trữ hết 102 ma trận cơ sở, thay vào đó chỉ cần lưu trữ 16 ma trận cơ sở ứng với mỗi một index \(i_{LS}\) ( mỗi một base graph có 8 ma trận dạng này). Ma trận này là ma trận cơ sở của \(Z_c\) lớn nhất trong mỗi index. Các ma trận cơ sở khác sẽ được tính toán “on-fly” dựa trên công thức. Điều này giúp giảm tài nguyên nhớ sử dụng.
- Để giảm hơn nữa tài nguyên nhớ, như đã phân tích ở trên, thực hiện mã hóa thông tin chỉ cần 4 thành phần của ma trận cơ sở là \(A, E, C_1, C_2\). Do đó, chỉ cần lưu trữ 4 ma trận thành phần trong một ma trận cơ sở mà thôi.
5. Precomputed base matrices
102 ma trận cơ sở của 5G LDPC có thể xem tại đây